[지수함수] - 우리가 코로나 확진자 수에 놀라는 이유

0. 들어가며

코로나를 미리 예상하신 명수옹?

2019.11.17 코로나19가 우리의 일상을 덮쳤다. 하지만, 한동안은 코로나19 이슈에도 불구하고 비교적 잠잠했었는데

 

그 이유는 2020년 3월 이후 한동안은 확진자 수가 100명 아래였기 때문이다. 

http://www.dt.co.kr/contents.html?article_no=2020052902109919607024&ref=naver 

"절대 K방역 못따라간다"...영국의학저널의 `절규`

(위풍당당했던 K방역)

 

한국의 코로나 방역을 극찬하는 2020년 5월의 기사다. 물론, 지금도 영국에 비해서는 훨씬 적은 편이다. (영국은 작년 연말 이후 확진자가 10만명 이상으로 늘어났다.) 

 

하지만, 행복은 그리 오래가지 못했다. 

https://newsis.com/view/?id=NISX20211221_0001696856&cID=10201&pID=10200 

오후 9시 전국 6314명 신규확진…최종 7000명대 예상

거리두기를 해제하며, 우리나라도 확진자가 7,000명 대를 돌파한 것이다. "언제 이렇게 코로나 확진자가 많이 늘어났지?" 이 당시 지인들과 나눴던 대화다.

 

그 이유는 "지수적 증가"라는 전염병이 가진 속성에 있다.

 

1. 선형이 주는 편안함(시몬스?)

그래프1과 그래프2 둘중에 뭐가 더 자연스러울까? 당연히 그래프 1이 자연스럽다. 그 이유는 그래프 해석 방식에 있다. 그래프1의 경우 이전만큼 증가했구나 라고 생각할 수 있다. 반면, 그래프2의 경우 3->4로 넘어갈 때 무슨 일 있었던 것 아냐? 라고 생각할 수 있기 때문이다.

 

이처럼 선형성은 예측하기 쉽다는 점에서 인간한테 편안함을 준다.

코로나바이러스감염증-19_확진환자_발생현황_220117.xlsx

0.19MB

질병 관리청의 데이터를 이용해서 2021.01.20 ~ 2021.05.20의 확진자수를 피팅해봤다.

 

import pandas as pd
import matplotlib.pyplot as plt
import scipy
import numpy as np
import seaborn as sns

data_raw = pd.read_csv("covid19_korea.csv", encoding="cp949")
data_linear_0120_0520 = data_raw.loc[(data_raw['일자'] >= "2021-01-20")&(data_raw['일자'] <= '2021-05-20')].copy()
data_linear_0120_0520['idx'] = data_linear_0120_0520.index - 365
data_linear_0120_0520 = data_linear_0120_0520.rename(columns={"계(명)":"confirmed cases"})

def annotate(ax, data, x, y):
    slope, intercept, rvalue, pvalue, stderr = scipy.stats.linregress(x=data[x], y=data[y])
    ax.text(.02, .9, f'slope={slope:.2f}, intercept={intercept:.2f}, r2={rvalue ** 2 : .2f}', transform=ax.transAxes)
    
plt.figure(figsize=(10, 5))
ax = sns.regplot(x='idx', y='confirmed cases', data=data_linear_0120_0520)
annotate(ax, data=data_linear_0120_0520, x='idx', y='confirmed cases')
plt.tight_layout()
plt.show()

편의상 2021.01.20을 1로 치환하여 날짜를 숫자로 표현하였다. Y축은 일별 확진자 수 이다. 선형 함수 피팅 결과는 다음과 같다. 

\begin{equation} y = 2.54x + 349.15 \end{equation}

이 함수를 이용하여 9월 말 경의 확진자 수를 예측해보자. 1월 20일 부터 대략 250일 가량 지났다고 가정하면

 

9월 말 경의 확진자 수는 다음과 같이 된다.

\begin{equation} 984.15 = 2.54*250 + 349.15 \end{equation}

대략, 984명 정도가 된다. 

하지만, 실상은 그렇지 않다. 9월 말경에는 확진자수가 2,000명을 넘어 3,000명 가량에 육박했었다. 불과, 2021년 6월 말까지만 해도 사람들은 코로나 확진자수가 1,000명이 넘을 것이라고는 생각하지 못했을 것이다. 왜나하면, 선은 그렇게 보이지 않았기 때문이다.

 

2. 지수적 증가란?

쉽게 생각해 어느 순간 증가에 가속도가 붙는 현상을 의미한다. 대표적인 사례로 복리 이자가 있다. 예를 들어서 은행 예금(100$)의 연이율이 5%일 경우 0년의 n년후 예금 금액은 다음과 같이 생각할 수 있다.

\begin{equation} 100*1.05^n \end{equation}

https://courses.lumenlearning.com/finitemath1/chapter/reading-compound-interest-and-exponential-growth/

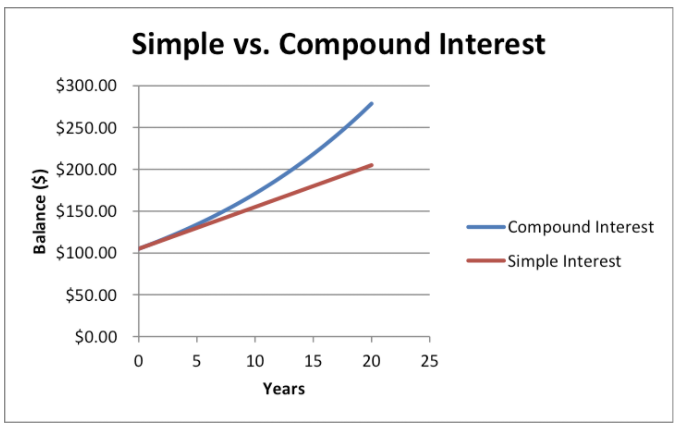
선형함수는 매번 일정하게 증가하는 반면, 지수 함수는 시간이 흐를수록 증가량에 가속도가 붙는다. 

 

다시, 코로나 데이터를 간단한 지수함수에 피팅해보자.

data_linear_After0120 = data_raw.loc[(data_raw['일자'] >= "2021-01-20")&(data_raw['일자'] <= "2021-12-16")].copy()
data_linear_After0120['idx'] = data_linear_After0120.index - 365
data_linear_After0120 = data_linear_After0120.rename(columns={"계(명)":"confirmed_cases"})

data_linear_After0120['curve_fit_value'] = data_linear_After0120.idx.map(lambda x : np.power(1.027, x) + 453)

plt.figure(figsize = (10, 5))
plt.plot(data_linear_After0120['idx'], data_linear_After0120['confirmed_cases']
         , 'o', label='origin_value')
plt.plot(data_linear_After0120['idx'], data_linear_After0120['curve_fit_value']
         , label='curve_fit_value')
plt.legend(loc='best')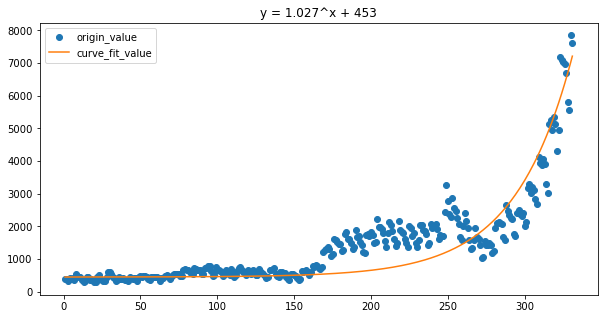

X축 = 확진자수, Y축 = 2021-01-20을 1로 치환

\begin{equation} y = 1.027^x + 453 \end{equation}

오버피팅이 과하기는 하지만, 지수형태에 상대적으로 좀 더 잘 피팅되는 모습을 보인다. 물론, 이 함수대로라면 당장 2월경만 되도 확진자수가 1만 5천명에 도달할 것이다.

 

3. 결론

코로나 확진자가 불과 100명 아래인 시절도 있었다. 그 시절에는 아무도 코로나 확진자가 1,000명이 넘을 것이라고 생각하지는 못했을 것이다. 결론적으로, 우리가 코로나 확진자 수를 보고 놀라는 이유는 확진자 수가 생각보다 빠르게 증가하기 때문이다. 지수적 증가의 무서움은 가속도에 있다. 전염은 절대 선형적으로 일어나지 않는다. 고삐를 늦추면 생각보다 빠른 시일 내에 다시, 우리의 목을 조일 것이다.