

- 본 글에서는 가설검정의 논리와 무작위 실험이 필요한 이유, 그리고 선택 편향에 대해서 다룹니다.
- P-value등 통계적인 개념에 대해서는 깊게 다루지 않습니다.
1. 가설검정
1-1. P-value와 영가설
- 연구자들은 P-value하나에 울고 웃는다.

- P-value가 0.05미만인 것을 왜 이렇게 좋아할까? 왜냐하면 영가설을 기각할 수 있기 때문이다.

1-2. 영가설이란?
- P-value는 “0.05미만이면 기분이 너무 좋다!” 정도로만 기억하고, 영가설(NULL HYPOTHESIS)이 무엇인지 알아보자.
- 여기서, 우리에게 친숙한 단어가 있다. 바로, “NULL”
- “NULL”은 “값이 없음”을 의미한다. → 즉, 영가설이란 = 가설이 없는 상태를 의미한다.
- 가설이 없다는 것은 다른 의미로 = “차이가 없음”을 의미한다.
- 차이가 없다는 것을 알기 위해서는 “비교”가 필요하다.

- 영가설이란 것은 어떤 대상을 비교 하기도 전에 “차이가 없을 것이라고 선언” 하는 것이다.
- 반대로, 대립가설은 어떤 대상을 비교 했을 때 “차이가 있을 것이라고 예상”하는 것이다.
- 즉, 가설검정의 영가설은 무죄추정의 원칙과 비슷하다.

그런데, 여기서 의문점이 든다. 차이가 있을 것 같으면 속시원하게 차이가 있다고 하면 되지,
왜 이런 표현을 사용하는 것일까?
- 그 이유는 우리가 평소에 하는 말싸움에서 찾을 수 있다

- 내 말이 맞다는걸 증명하는 것은 어렵지만, 맞다는 말을 반박하기는 쉽다. 왜냐하면, 틀렸다는 사례 한 가지만 찾으면 되기 때문이다.
- 예를 들어서, 판교초 3학년 6반 병재가 “나보다 팔씨름 잘하는 초딩 있으면 나와!”라고 했다고 하자.
- 병재는 평생 본인의 가설을 증명할 수 없다.
- 왜냐하면, 죽을 때 까지 모든 초딩들과 팔씨름을 붙어서 다 이겨야 하기 때문이다.
- 하지만, 병재의 가설은 반박하기 쉽다. 팔씨름 잘하는 초딩 한명 찾으면 그만.
그것이 우리가 대립가설을 이용해서 영가설을 기각하는 이유다. 왜냐하면, 맞다는 말을 증명하는 것보다 맞다는 말을 반박하는 것이 더 쉽기 때문이다.
2. 실험
2-1. 실험의 목적
- 실험의 목적은 내가 생각한 가설이 맞는지 확인하는 것이다.
- 앞서 가설검정은 영가설을 대립가설로 기각하는 구조를 가지고 있다고 하였다.
- 그러기 위해서는 아래 두 집단에 대한 비교가 필요하다.
- 실험군 - 특정 처치를 가한 집단
- 대조군 - 아무것도 하지 않은 집단
실험군과 대조군 간의 차이 없음 → 영가설 지지 → 실험 실패
실험군과 대조군 간의 차이 있음 → 영가설 기각 → 실험 성공!
2-2. 선택 편향
- 뽑고 봤는데 다 비슷한 사람?

- 분석 공부를 했던 사람들에게는 매우 유명한 타이타닉 데이터 셋이다.
- 타이타닉호에서 생존 확률은 여성이 남성보다 더 높았다.
- 한 가지 흥미로운 점은 모델에 “성별”이라는 변수 하나만 넣어도 예측 정확도가 80% 가까이 나온다는 것이다.
https://www.kaggle.com/code/pliptor/optimal-titanic-for-gender-only-0-7655/report
Optimal Titanic for Gender only [0.7655]
Explore and run machine learning code with Kaggle Notebooks | Using data from Titanic - Machine Learning from Disaster
www.kaggle.com
- 심리학 분야의 연구에 대해 흔히 제기되는 문제 중에 대학교 2학년 문제(College sophomore problem)가 있다.
- 졸업을 하기 위해서는 어떻게든 실험을 하고 결과를 내야 하는데,
- 그 실험에 참여하는 학생들이 “가산점이 필요한 2학년 심리학 수업 수강생”이라는 것이다.
이처럼 표본에 속하는 사람들이 공통적으로 가지고 있는 특징이 있다면, 실험 결과를 제대로 신뢰할 수 없게 된다. 왜냐하면, 실험 결과가 표본에 속하는 사람들이 공통적으로 가지고 있는 특징에서 기인했을 수 있기 때문이다.
- 이와 같은 현상을 “선택 편향”이라고 한다.
2-2. 무작위 실험
- 무작위 실험이란 말 그대로 무작위로 사람들을 뽑아서 실험군과 대조군에 할당하는 것이다.(=무선할당)
- 왜 이렇게 하는걸까? 좀 더 명확한 설명을 위해 잠시 교재의 수식을 참고하겠다.(고수들의 계량경제학)
- 예시 상황

- 위와 같은 상황을 가정해보자. 그렇다면 여기서 실험 효과란 아래와 같이 정의할 수 있다.
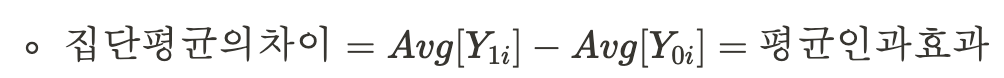
- 그렇지만, 보이는게 전부 다가 아닐 수 있다.
- 예를 들어, 후방 카메라의 효과에 대한 실험을 가정해보자.
- 실험 결과, 실험군의 후방 카메라 사용 전/후 운전 실력에는 큰 변화가 있었지만
- 대조군의 운전 실력에는 큰 변화가 없었다고 하자.
- 그런데, 알고 봤더니 실험군에 있던 사람들이 모두 운전 초보자였던 것이다.
- 이를 수식으로 다시 표현하면 아래와 같이 된다.
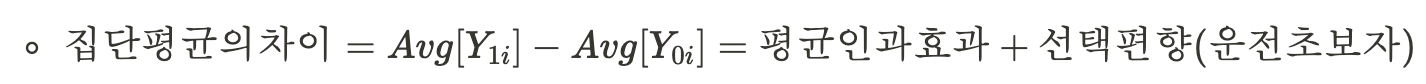
이러한 선택편향을 최소화하기 위해 무선할당을 진행한다.
- 무선할당을 하게 되면 실험군과 대조군 개별 참여자들 간에 차이가 있을 수는 있다.
- 하지만, 운전초보자와 고수가 고르게 섞여 있을 것이므로 집단 평균적으로는 차이가 없게 된다.
- 이를 통해, 선택편향을 제거하고 나면 아래와 같은 진정한 인과효과를 볼 수 있게 되는 것이다.
- 무선할당만 하면 모든 통제가 완료된 것일까?
- 당연히 그렇지 않다.
- 실험 환경도 통제해야 한다. 대표적인 예로 호손실험이 있다.

- 실험에서 뭔가 발견한듯 싶었지만.. 실상은 누군가(실험자)가 내가 일하는 걸 보고 있어서 열심히 한 것일뿐.. 물론 그 자체로도 큰 발견이긴 하다
- (아들 공부 열심히 하고 있지?)
Ref
고수들의 계량 경제학
행동과학을 위한 통계학
https://www.massgeneral.org/neurology/als/research/placebo-trials
Placebo-Controlled Trials
Every ALS researcher has been asked the very reasonable question: why use placebos in a trial for a disease as serious as ALS?
www.massgeneral.org
https://www.cancer.gov/publications/dictionaries/cancer-terms/def/double-blind-study
NCI Dictionary of Cancer Terms
NCI's Dictionary of Cancer Terms provides easy-to-understand definitions for words and phrases related to cancer and medicine.
www.cancer.gov
https://www.wikiwand.com/en/Selection_bias
Wikiwand - Selection bias
Selection bias is the bias introduced by the selection of individuals, groups, or data for analysis in such a way that proper randomization is not achieved, thereby failing to ensure that the sample obtained is representative of the population intended to
www.wikiwand.com
'딥상어동의 딥한 통계학' 카테고리의 다른 글
| 왜 단절이라는 말을 사용하는 건가요? - 회귀 단절 모형 (0) | 2023.04.02 |
|---|---|
| 평균으로의 회귀, 그리고 변수 통제 (2) | 2023.02.05 |
| 분포를 살펴보는 이유 (0) | 2022.06.25 |
| 두번 빼면 인과 효과가 보이는 이유 - 이중차분법(Difference in Difference) (0) | 2022.04.22 |
| 내생 변수(endogenous variable) - 하늘 아래 태양은 하나다. (0) | 2022.04.15 |

제 블로그에 와주셔서 감사합니다! 다들 오늘 하루도 좋은 일 있으시길~~
포스팅이 좋았다면 "좋아요❤️" 또는 "구독👍🏻" 해주세요!



