

본 글은 "고수들의 계량경제학"을 참고하여 작성하였습니다.
1. 평균으로의 회귀
비트코인 랠리 평균가 회귀
번스타인 비트코인 랠리는 평균가 회귀 현상한계 분명해 | 한국경제TV (wowtv.co.kr)
💡 비트코인이 미국 연방준비제도(Fed·연준)의 금리인상 속도 조절 기대감에 상승세를 이어가고 있는 가운데 글로벌 IB(투자은행) 번스타인이 비트코인 상승 랠리의 허점을 지적하고 나섰다.
23일(현지시간) CNBC에 따르면 번스타인은 "비트코인 상승 랠리가 장기적인 평균 가격으로 돌아가는 일시적인 반등에 불과하다"면서 "상승 랠리를 유지하기 위한 근본적인 동력이 부족하다"고 밝혔다. 이날 고탐 추가니(Gautam Chhugani) 번스타인 애널리스트는 고객들에게 보낸 서한에서 최근 암호화폐 시장에서 나타나고 있는 비트코인 상승 랠리가 평균 회귀(Mean Reversion) 현상에 불과하다고 강조했다.
- 현실의 많은 현상들은 정규분포를 따른다.
- 정규분포에서 평균 -3표준편차 ~ 평균 + 3표준편차 사이에 99.7%의 모든 케이스가 포함
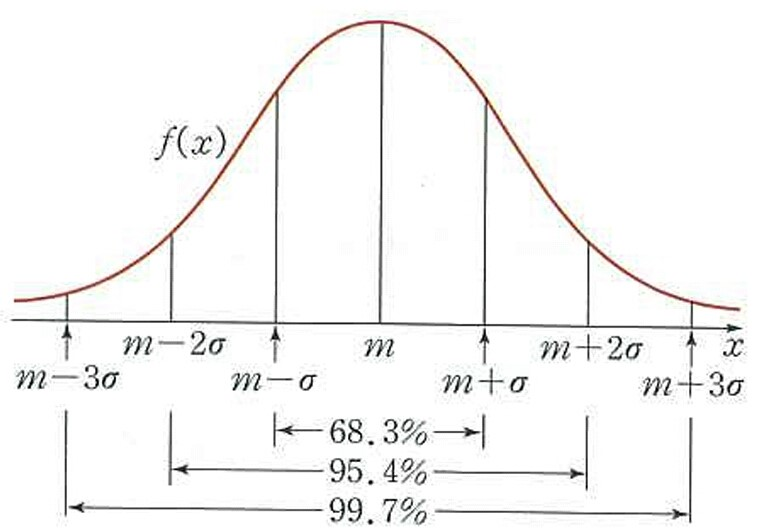
- 즉, 0.3%에 해당하는 극단적인 케이스는 소수이며 대다수의 사례는 평균 주변으로 밀집한다.
부모의 키가 크면 자식의 키도 클까?
재앙을 부르는 판단의 함정⑥ 평균으로의 회귀 : 네이버 블로그 (naver.com)

- 만약, 부모의 키가 자식의 키와 정비례한다면 회귀식은 검은색 선과 같이 일직선으로 될 것이다.
- 하지만, 확인 결과 부모의 신장 평균과 자녀의 신장 평균의 교차하는 지점에서
- 키가 큰 부모의 자식들은 부모보다 키가 작아지고, 키가 작은 부모의 자식들은 부모보다 키가 커지는 현상을 발견했다.
- 이를 평균으로의 회귀라 하며, 이는 위에서 설명한 현실 세계의 분포의 안정성에 기반한다.
우승자 징크스
마지막 스타1리그 우승자 허영무 … 사상 최고 2회 연속 우승 - 헬스코리아뉴스 (hkn24.com)
'디펜딩 챔피언 저주' 이번에도?…역대 월드컵 징크스 모아보니 | 중앙일보 (joongang.co.kr)

- 우승자 징크스가 실제로 존재할 수도 있지만, 혹시 평균으로의 회귀는 아닐까?
2. 통제 - 왜 해야 하는가?
책에서 말하는 회귀 모형의 목적
- 무선할당이 힘들 때,
- 회귀분석은 처치집단과 통제집단간의 핵심적인 관측변수들을 동일하도록 만들어
- 우리가 볼 수 없는 것들로부터 발생하는 선택 편의를 제거하고
- 제거한 선택 편의를 바탕으로 인과 효과를 추정한다.
통제의 난이도
- 물뿌리기, 물안뿌리기 VS 세금올리기, 세금안올리기

- 현실의 문제는 물뿌리기처럼 간단하지 않다.
통제를 하지 않았을 때 발생할 수 있는 문제
- 책에서는 하버드대학교 졸업생과 메사추세츠대학교 졸업생의 소득격차에 대해 얘기하고 있다.
-단순 소득격차를 비교하면, 하버드 졸업생들의 고등학교 성적이 일반적으로 뛰어나고 / SAT 점수가 높고 / 의욕도 높을 것이기에 당연히 하버드대학교 졸업생의 소득이 높을 것이라는 것
- 현실에서는 어떨까?
- 실제로 대학 진학은 부모의 월평균 소득과 높은 연관성을 가진다. 또한, 부모의 학력 수준과도 높은 연관성을 가진다.
KDI“부모 학력-소득과 자녀성적은 비례” (donga.com)

책의 용어를 빌리자면, 여기서 부모의 소득과 학력 수준은 통제해야할 변수이다.
3. 통제 - 어떻게 해야 하는가?
선택 편향과 우연한 차이
- 앞서 얘기했던, 졸업학교는 선택편향을 유발할 수 있다.
- 여기 suzy라는 사람이 있다.

- suzy의 고향은 텍사스 출신으로 하버드대학교, 텍사스대학교에 모두 합격했지만 재정 지원을 해주는 텍사스대학교에 입학했다.
- 여기 jaehoon이라는 사람이 있다.

- jaehoon의 고향은 어딘지는 모르겠지만 하버드대학교에 입학했다고 한다.
- 만약, 이 둘을 비교한다면? 선택편향이 발생했다고 할 수 있을까? 그렇지 않다.
왜냐하면, 출신 대학교 외에도 학업 성취도라는 변수를 통제했기 때문이다.
- 책에서는 이를 우연한 차이라고 설명한다.
- 그리고, 이렇게 매칭된 비교 쌍을 좋은 짝이라고 표현한다.
통제 조건
- 우연한 차이의 핵심은 변수를 어떻게 통제하는지에 있다.
- 책에서는 사립학교 입학이 향후 소득수준에 미치는 영향을 확인하기 위해 변수 통제를 진행하였다.
- 위와 같은 조건을 책에서 행렬로 구현해놓은 표이다.
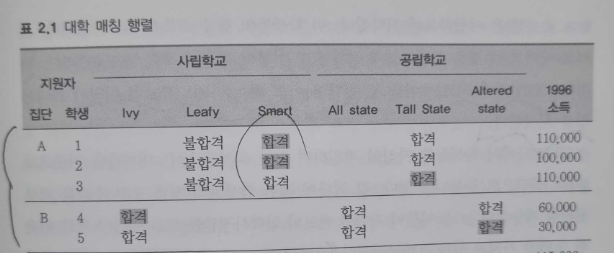
- 집단A와 집단B는 다음 두 가지의 조건을 가지고 있다.
1. 사립학교와 공립학교 모두 합격했다.
2. 모두 합격후 사립학교를 선택한 사람과 공립학교를 선택한 사람이 나뉘어져 있다.
가중평균과 통제

- 가중평균에는 기본적으로 통제(입학대학종류)라는 개념이 깔려있다. 이 때, 소득차이평균은 계산 방식에 따라 9000달러, 12500달러이며 이는 통제하지 않았을 때 소득차이평균인 20000달러와 차이를 가진다.
- 즉, 통제를 하지 않았을 때 추정치에 선택편향이 반영 되는 것을 알 수 있다.
회귀 모형 해석
- 회귀 모형을 사용하는 이유
- 회귀계수의 추정치는 통제 조건들을 반영한 가중 평균값이기 때문

- 여기서 beta가 10000이라는 것은 사립학교와 공립학교의 소득차이가 10000달러라는 것을 의미한다. 이 값은 앞서 구한 가중평균 9000달러와 12500달러 사이에 위치한다.
- 그리고, 이 값은 단순 평균인 20000달러 보다는 훨씬 작은 수치이다.
Ref.
'딥상어동의 딥한 통계학' 카테고리의 다른 글
| 인과추론이 분석에 날개를 달아주려면 (feat. 사내 스터디 후기) (8) | 2023.06.09 |
|---|---|
| 왜 단절이라는 말을 사용하는 건가요? - 회귀 단절 모형 (0) | 2023.04.02 |
| 가설검정과 무작위 실험 그리고 선택 편향 (0) | 2023.01.14 |
| 분포를 살펴보는 이유 (0) | 2022.06.25 |
| 두번 빼면 인과 효과가 보이는 이유 - 이중차분법(Difference in Difference) (0) | 2022.04.22 |

제 블로그에 와주셔서 감사합니다! 다들 오늘 하루도 좋은 일 있으시길~~
포스팅이 좋았다면 "좋아요❤️" 또는 "구독👍🏻" 해주세요!



