![[Boxplot] 박스플롯 이용시 주의사항](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FehG3yj%2FbtrohUbtCFz%2Fcs7FexdtRhZ5gKexdHeMJ0%2Fimg.png)

최근 글에서 박스플롯을 사용하여 분석 결과를 설명한 적이 있습니다.
https://gibles-deepmind.tistory.com/95
[데이터로 보는 주식] 물타기 도대체 언제 할것이냐, 그것이 문제로다.
0. 들어가며 안녕하십니까 파란불 달인 딥상어동입니다. 왜 파란불이라는 말을 썼을까요? 그것은 바로바로. 제 주식 포트 폴리오에 "음봉"이 가득~ 하기 때문인데요. 제 손으로 적기는 정말 슬픕
gibles-deepmind.tistory.com

일단은 시간은 없고.. 글은 빨리 마무리해야하니 박스플롯으로 결과를 설명했었는데요. 결과를 직관적으로 전달하지 못한다는 생각이 들었었습니다. 그리고, 이후 박스 플롯의 어떤 측면 때문에 정보를 직관적으로 전달하기 어려운지에 대해 고민해봤습니다.
1. 장점 - 정보량
우선 박스 플롯의 장점은 "다양한 정보를 손쉽게 표현할 수 있다"는 것입니다. 그렇다면, 박스플롯에는 어떤 정보가 담겨있을까요?
1. ......
2. 75%의 값
3. 중앙값
4. 25%의 값
5 ......
(100%에 가까울수록 큰 값입니다.)
즉, 값을 정렬했을 때 위치 값을 바탕으로 분포를 요약해서 표현한다고 할 수 있습니다. 그런데, 여기서 1번과 5번을 비워뒀는데요. 왜냐하면, 표현 방법에 따라서 1번과 5번의 값이 달라질 수 있기 때문입니다.
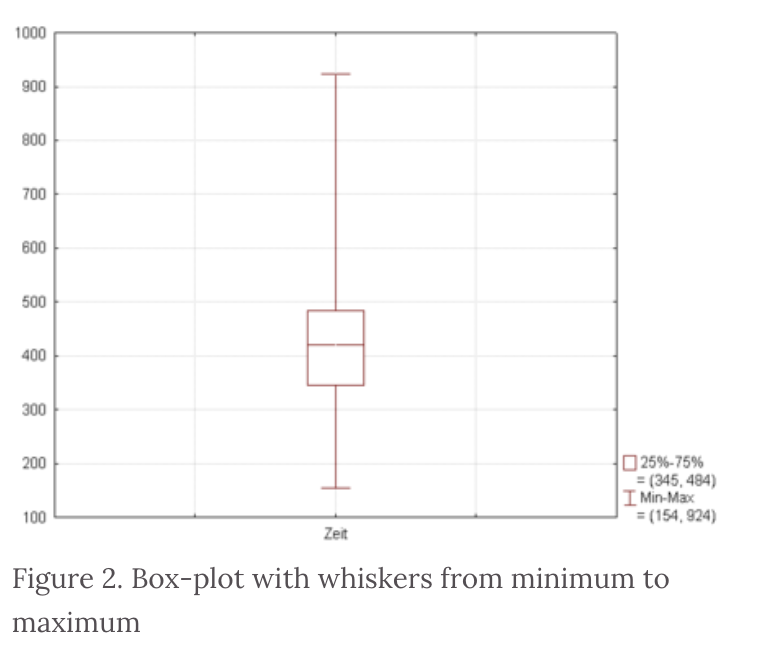
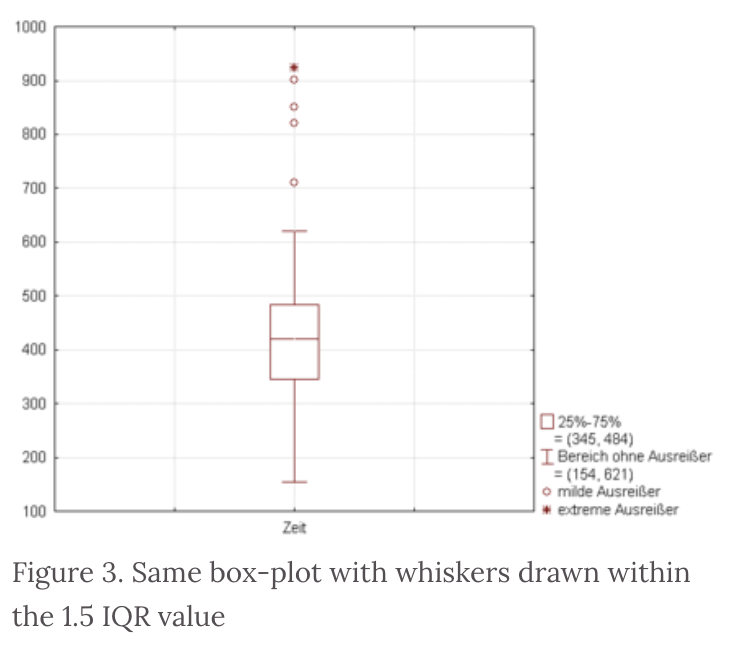
figure2와 figure3은 똑같은 데이터를 이용하여 박스플랏을 이용하였습니다만 시각화 결과는 다릅니다. 좌측의 경우 최솟값과 최댓값이 사용된 반면 우측의 경우 IQR이라는 개념이 사용되었기 때문입니다.
IQR = 75%값 - 25%값 (100% = MAX)
| Five number summary | Tukey style(1970) | Spear style(1952) |
| 상한 | 75% + 1.5IQR | MAX |
| 3분위수 | 75% | 75% |
| 중앙값 | 중앙값 | 중앙값 |
| 1분위수 | 25% | 25% |
| 하한 | 25% - 1.5IQR | MIN |
IQR이라는 개념이 들어가냐 안들어가느냐에 따라서 상한과 하한의 값이 달라질 수 있습니다. 사실, Boxplot을 처음 개발한 사람은 Spear라는 사람입니다. Spear가 처음 개발했을 당시 박스 플랏의 범위는 MIN~MAX 였으나, 이후 Tukey라는 사람이 IQR이라는 개념을 도입하며 지금 흔히 부르는 상자-수염 그림이라는 개념이 정립되게 됐습니다. 가장 큰 특징점으로 Spear style에서는 이상치를 표현할 수 없다는 특징이 있습니다. 저는 seaborn의 boxplot을 사용했었는데요. 한번, 파라미터를 살펴 보겠습니다.
whis : float, optional
Proportion of the IQR past the low and high quartiles to extend the plot whiskers. Points outside this range will be identified as outliers.
seaborn의 boxplot에는 whis라는 IQR파라미터가 있고, default 1.5로 설정되어 있습니다. 즉, seaborn의 boxplot을 사용하면 IQR 개념을 이용하여 boxplot을 그려준다고 할 수 있습니다. whisker의 약자를 따서 whis라고 파라미터 이름을 정한것 같네요.
2. 단점 - 정보량
하지만, 단점도 "정보량"이라고 할 수 있습니다. 왜냐하면, 그 정보를 읽어야하기 때문입니다.

북반구의 여름기온분포입니다. 여름기온분포라는 말 한마디만 들어도, 1951 ~ 1980년에는 지구 온난화가 본격적으로 시작 되지는 않았구나라는 사실을 이해할 수 있습니다.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sample_df1 = pd.DataFrame(np.random.normal(0, 1, 1000), columns = ['stanNormalDist'])
plt.figure(figsize=(8, 5))
plt.title("1951-1980 Summer temperatures in the Northern Hemisphere")
sample_df1.boxplot();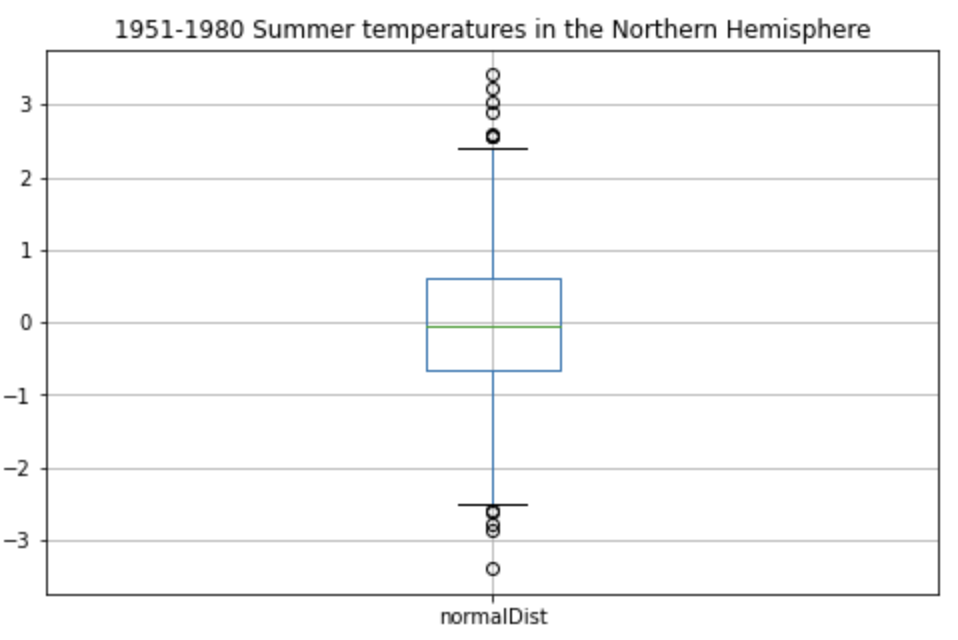
1951-1980 북반구 여름 기온 분포를 박스 플롯으로 나타내봅시다(데이터는 표준정규분포에서 랜덤하게 뽑았습니다). 이해가 잘 가시나요? 분포에서 본 것과 같이 cold와 hot영역을 색상으로 칠할 수 있을까요? 어렵습니다. 왜 그럴까요?
3. 분포와 박스 플롯의 차이점
분포를 통해 저희가 파악할 수 있는 정보는 무엇인가요?

다시, 북반구 여름기온 분포를 봅시다. Normal영역을 중심으로 값이 몰려 있다는 것을 알 수 있습니다. 즉, Normal영역을 중심으로 값이 몰려 있구나! = 기온이 정상적이구나! 라는 판단을 할 수 있습니다. 그러면, 이러한 판단은 어디서 기반할까요?
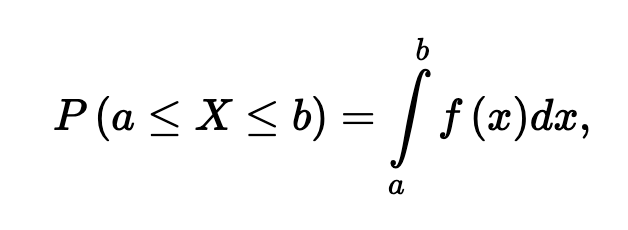
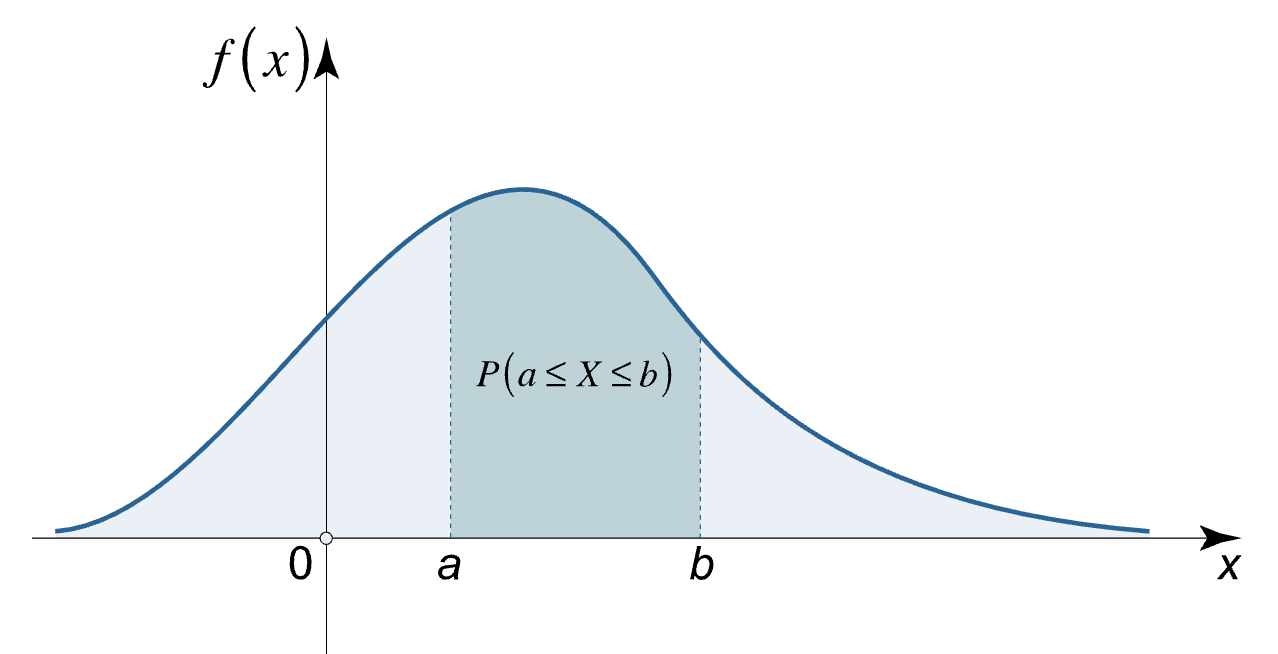
확률밀도함수에서 확률은 "넓이" 입니다. 즉, 분포의 넓이를 보고 값이 많이 몰려 있구나라는 판단을 하게 됩니다. 사실, 복잡한 적분 공식도 필요 없습니다. 영역의 넓이만 살펴보면 되니 매우 쉽죠.
그렇지만, 박스 플롯은 확률 정보를 직관적으로 표현하지 못합니다. 박스 플롯은 기본적으로 "위치 정보"에 기반하고 있습니다. 박스 플롯을 공부한 사람도 박스 플롯이 표현하는 분포를 이해하기 위해서는 고민이 필요합니다.
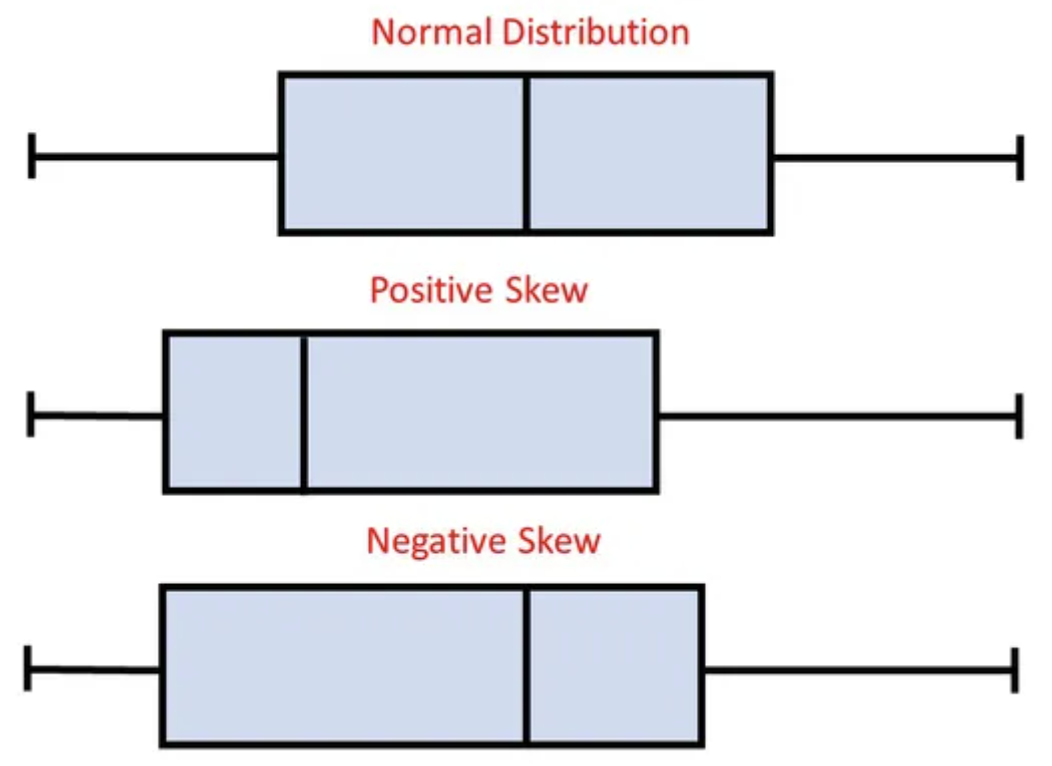
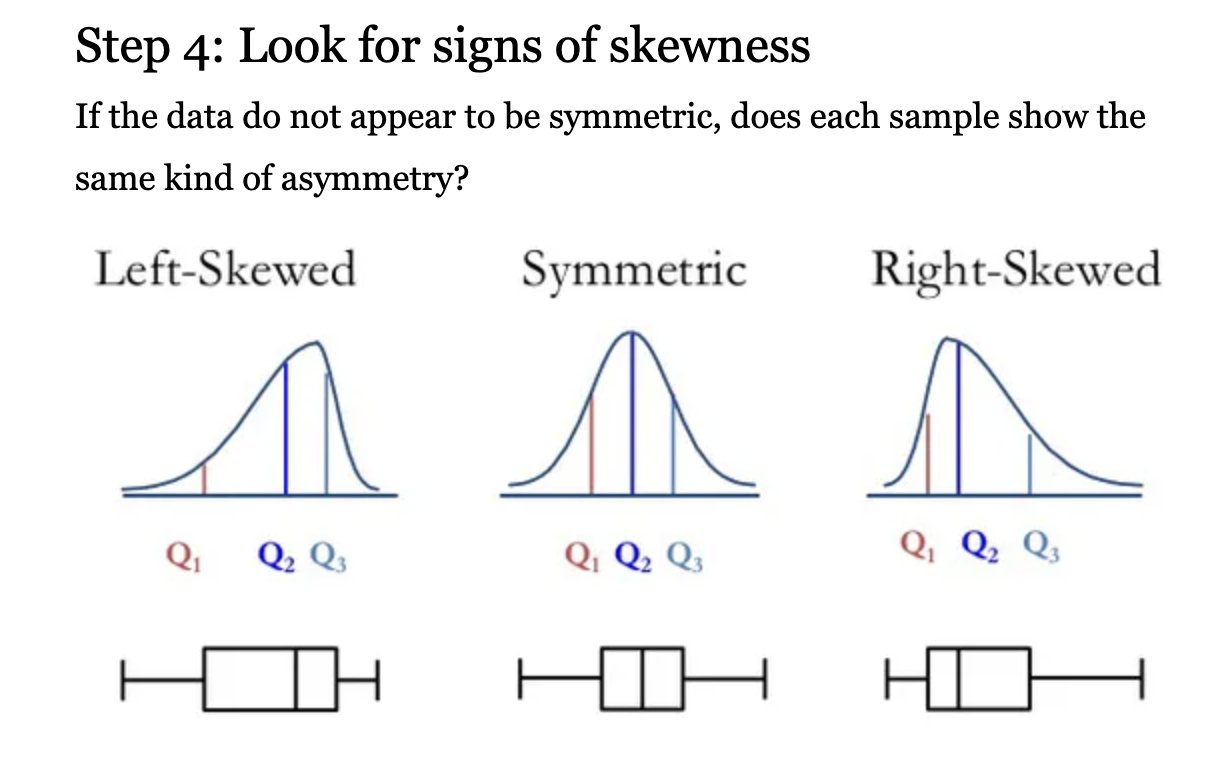
왼쪽 그래프를 보고 박스 플롯을 처음 들어보는 사람이 Positive Skew가 무엇인지, Negative Skew가 무엇인지 이해할 수 있을까요? 아마 오른쪽 그림처럼 분포 범례를 보여주지 않으면 이해하기 어려울 것입니다.
4. 박스 플롯은 정규분포가 아니다.
또, 한가지 주의해야할 점은 박스플롯은 정규분포가 아니라는 것입니다. 정규 분포의 특징 중 하나는 평균 = 중앙값 = 최빈값이 모두 같다는 것입니다.
박스플롯으로 설명을 하다보면 가끔 가장 가운데 선이 평균이냐는 질문을 받습니다. 하지만, 박스플롯은 정규분포가 아닙니다. 박스플랏의 가운데 선은 중앙값입니다. 경우에 따라 평균과 같을 수도 있습니다. 하지만, 평균과 같지 않을 수도 있습니다.
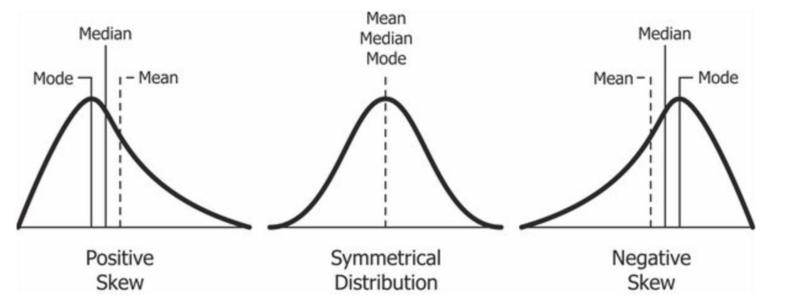
그리고, 소름 돋는건 저 자신도 글을 적다보면 중앙값을 평균이라고 표현할때가 있다는 것입니다. 어쨌든, 박스플롯은 정규분포가 아닙니다.
5. 결론 - 박스플롯은 분포를 정확하게 표현하지 못한다.
결론적으로 박스플롯은 분포를 정확하게 표현하지 못한다고 할 수 있습니다. 때로는, 이 단점이 치명적일 때가 있는데요. 예시를 하나 들어보겠습니다.
N = 1000
mu1, sigma1 = 0, 1
mu2, sigma2 = 9, 1
X1 = np.random.normal(mu1, sigma1, N)
X2 = np.random.normal(mu2, sigma2, N)
X_bimodal = np.concatenate([X1, X2])
X_uniform = np.random.uniform(min(X_bimodal), max(X_bimodal), N*2)
#데이터프레임 생성
sample_df2 = pd.DataFrame()
sample_df2['bimodal'] = X_bimodal
sample_df2['uniform'] = X_uniform
sample_df2.boxplot()
각 변수별로 상자 그림을 그려보겠습니다.
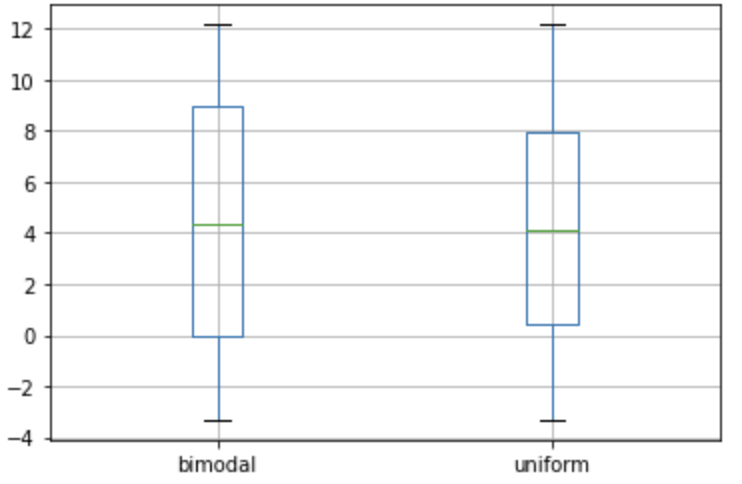
거의 비슷해보이죠?
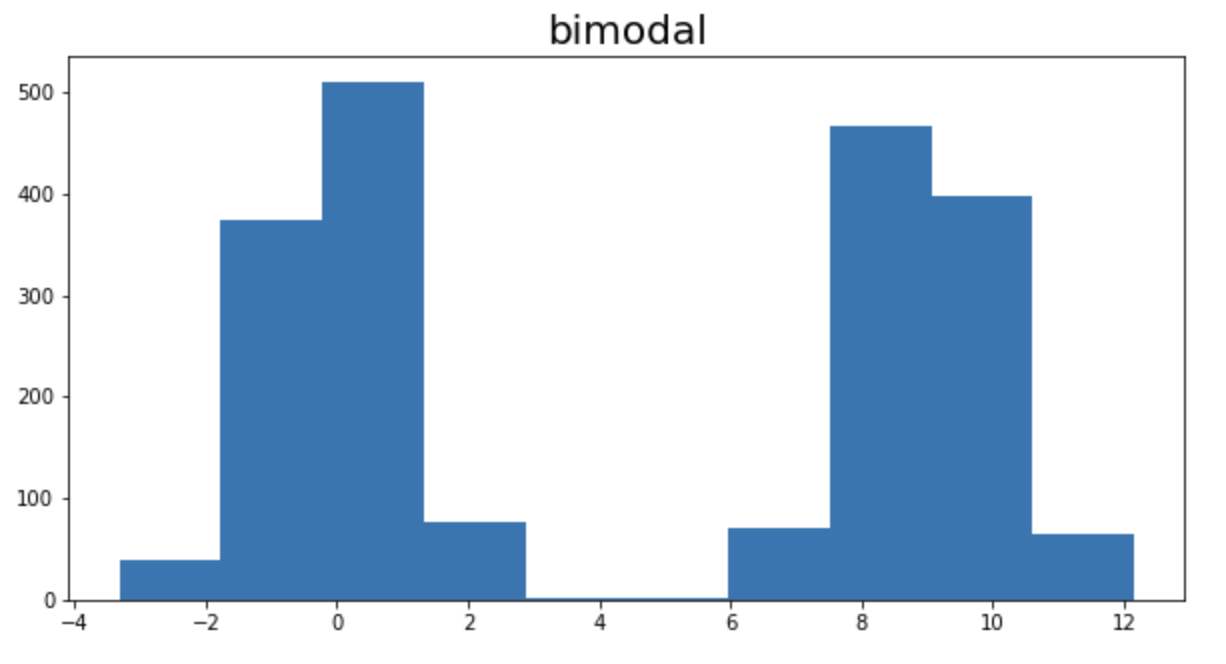
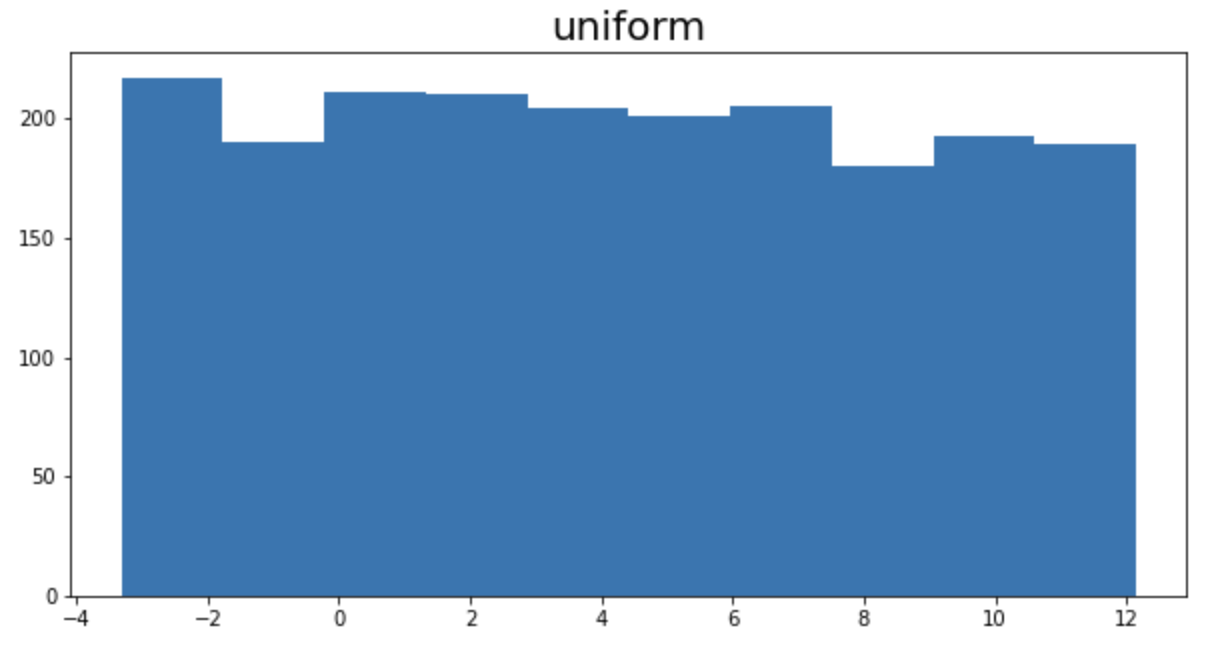
하지만, 히스토그램을 그려보면 완전히 다른 분포라는 사실을 알 수 있습니다. 결론적으로, 박스플롯은 분포를 정확하게 표현하지 못합니다. 그리고, 때로는 이러한 특징 때문에 해석시 오해가 있을 수도 있습니다.
6. 박스 플롯 보완하기
sample_df3 = pd.DataFrame([1, 3, 5, 7, 9], columns=['5points'])
sample_df3.boxplot();
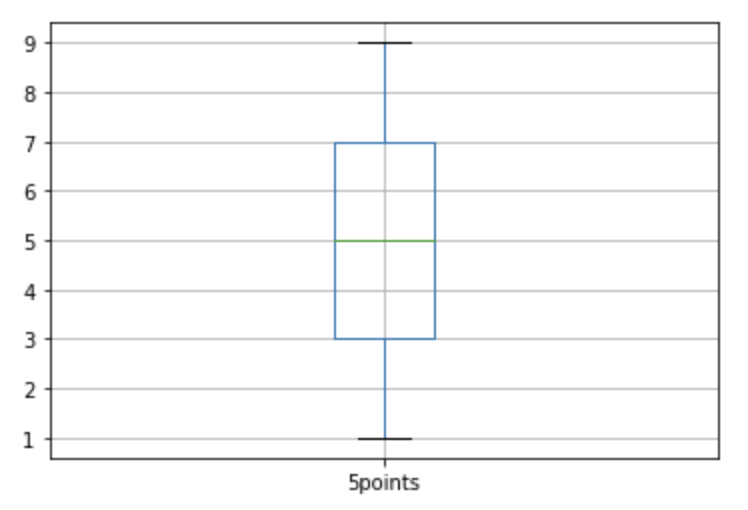
사실, 점5개만 있으면 그릴 수 있는게 박스 플롯입니다. 저 상자안에 대단한 정보가 담겨 있을 것 같지만, 실상은 점 5개 밖에 없는 그래프에 불과할 수 있습니다(물론, 점 5개도 의미 았을 수 있습니다). 그렇다면, 어떻게 박스 플롯을 보완할 수 있을까요?
6-1. 박스플롯을 점과 함께 그리기
첫 번째로 박스 플롯을 점과 함께 그리는 방법이 있습니다.
#박스 플롯을 우선 그리고
sample_df2.boxplot()
#matplotlib을 이용하여 그 위에 각 점들을 찍어줌
for i, d in enumerate(sample_df2):
y = sample_df2[d]
x = np.random.normal(i + 1, 0.04, len(y))
plt.scatter(x, y)
plt.title("boxplot with scatter", fontsize=20)
plt.show()
6-2. Ridge line plot 그려보기

다음으로, 분포를 각 속성별로 그려볼 수 있는 Ridge Line Plot이 있습니다.
https://www.analyticsvidhya.com/blog/2021/06/ridgeline-plots-visualize-data-with-a-joy/
Ridgeline Plots: Visualize Data with a Joy! | What is Ridgeline Plot?
Ridgeline Plots or Joy Plots is a kind of chart that is used to visualize distributions of several groups of a category in the data
www.analyticsvidhya.com
joypy를 이용하면 손쉽게 해당 그래프를 그려볼 수 있는데요. 위 링크를 한번 참고하시면 좋을 것 같습니다.
https://jehyunlee.github.io/2020/09/07/Python-DS-30-mpl_dists/
Ridgeline Plot
시간의 흐름에 따른 분포 추세 변화를 보여줍니다. matplotlib 혼자만으로는 힘듭니다. seaborn의 도움을 받아봅시다. pandas의 도움을 받을 수도 있습니다. Claus Wilke, “데이터 시각화 교과서”, 영문
jehyunlee.github.io
좀 더 다양하게 커스텀을 해보고 싶으시면, 이제현님의 블로그 링크도 한번 참고해보시면 좋을 것 같습니다. 개인적으로, 실무에서 사용했을 때 반응이 나쁘지 않았던 그래프 형태입니다.
6-3. 바이올린 플롯 이용하기
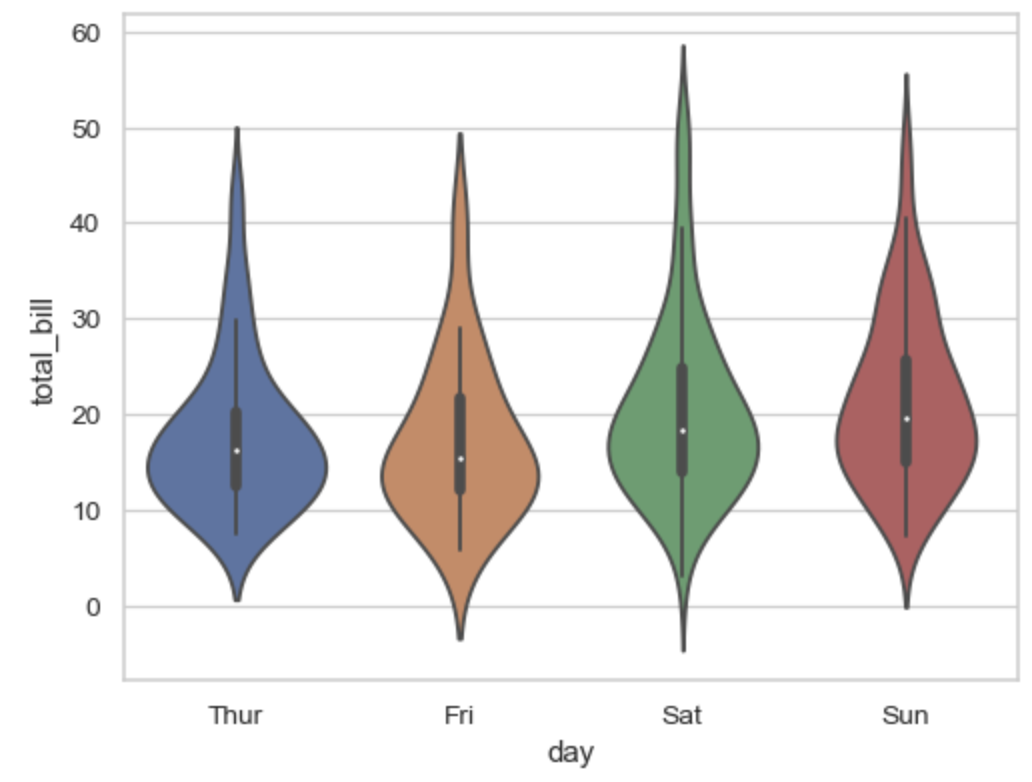
https://seaborn.pydata.org/generated/seaborn.violinplot.html
seaborn.violinplot — seaborn 0.11.2 documentation
The method used to scale the width of each violin. If area, each violin will have the same area. If count, the width of the violins will be scaled by the number of observations in that bin. If width, each violin will have the same width.
seaborn.pydata.org
마지막은 seaborn의 바이올린 플롯입니다.
Ref.
https://math24.net/probability-density-function.html
Probability Density Function
We call \(X\) a continuous random variable if \(X\) can take any value on an interval, which is often the entire set of real numbers \(\mathbb{R}.\) Every continuous random variable \(X\) has a probability density function \(\left( {PDF} \right),\) written
math24.net
https://www.simplypsychology.org/boxplots.html
Box Plot | Simply Psychology
In statistics, dispersion (also called variability, scatter, or spread) is the extent to which a distribution is stretched or squeezed. The smallest value and largest value are found at the end of the ‘whiskers’ and are useful for providing a visual in
www.simplypsychology.org
https://www.nature.com/articles/nmeth.2813
https://www.wikiwand.com/en/Box_plot
Box plot | Wikiwand
In descriptive statistics, a box plot or boxplot is a method for graphically demonstrating the locality, spread and skewness groups of numerical data through their quartiles.[1] In addition to the box on a box plot, there can be lines extending from the bo
www.wikiwand.com
https://stat.mq.edu.au/wp-content/uploads/2014/05/Can_the_Box_Plot_be_Improved.pdf
'딥상어동의 딥한 데이터 처리 > 시각화' 카테고리의 다른 글
| 분당선 정자역에서 생각해본 데이터 시각화의 단상 (0) | 2023.01.09 |
|---|---|
| [Pandas] 데이터프레임도 이미지로 저장할 수 있다구? (1) | 2022.10.02 |
| [Pandas] 퍼널차트 데이터프레임으로 표현해보기 (2) | 2021.08.15 |
| Seaborn | countplot(기본 파라미터, x축 정렬하기, x축 라벨 회전) (0) | 2021.03.07 |
| [Matplotlib] 모두를 위한 Python시각화 - (1)Matplotlib.artist (2) | 2021.01.03 |

제 블로그에 와주셔서 감사합니다! 다들 오늘 하루도 좋은 일 있으시길~~
포스팅이 좋았다면 "좋아요❤️" 또는 "구독👍🏻" 해주세요!

![[Pandas] 데이터프레임도 이미지로 저장할 수 있다구?](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FIeyHv%2FbtrNyEChk5v%2F7SXQ7hGKKOWXkpmQoa1NXk%2Fimg.png)
![[Pandas] 퍼널차트 데이터프레임으로 표현해보기](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fd4bGge%2Fbtrb6T4hpKK%2FVE6Zk7JYw7HgAZL1PSwlr0%2Fimg.jpg)
